バリュー平均法について、独自にシミュレーションして分かったこと。

こんにちは。林FP事務所の林です。
岡本氏の著書「確定拠出年金 最良の運用術」で紹介されてから、各ブロガーさんで話題になっていたバリュー平均法ですが
独自にシミュレーションしてみました。
結論として一部苦手な局面もあるようで、通常のドルコスト平均法で十分かなと思います。
バリュー平均法の投資シミュレーション
バリュー平均法の詳しい説明については
岡本氏の著書「確定拠出年金 最良の運用術」を
参考にしてください。
著書内でもバリュー平均法のシミュレーションがありますが、
自分でやってみないと納得できない性格のため
独自にシミュレーションしてみました。
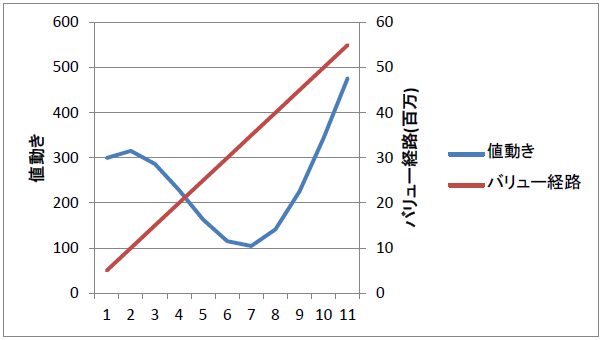
1. 右肩上がり1
シミュレーションの条件はこちら。
初期資産、買い付け額が少々大きめですが
シミュレーションぐらいは景気よく行きたいな
と思いましてw
以下ご自身の状況に合わせて額を読み替えてください。
まず青線の値動き(左軸)をする資産に、
バリュー経路(右軸)に沿ってバリュー平均法を使って投資する場合を考えます。
投資の損益率はこちら。
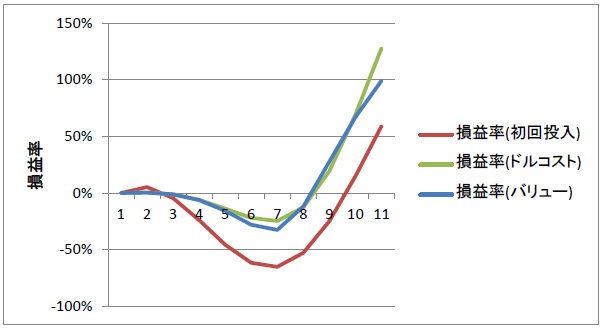
ここでいう損益率とは、初期資産6千万に対して、
±何%になったか、というもの。
例えば初回全額投入(赤)のパフォーマンスが
+59%ですが、この場合
資産は 6千万x1.59=9千5百万
になったということです。
あれ?
ドルコストがトップ、バリュー平均法が2番手です。
なんだか、バリュー平均法ってそんなにすごくないのかな?
と思いますね…。
2. 右肩上がり2
もしかしたら期間が短いせいかと思い、
もうすこし期間を延ばして20回投資します。
値動きもジグザグしながら平均的に右肩上がりとし、
バリュー経路は8千万までとしました。
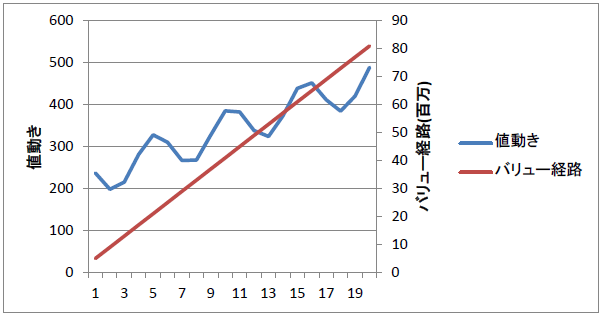
ドルコスト平均法は初期資産を
20回に分けて投入していきます。
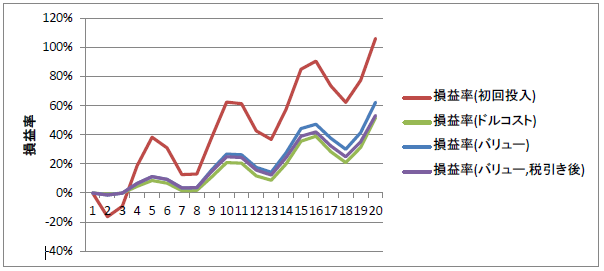
初回全額投入(赤)のパフォーマンスがダントツですが、
マイナス幅も大きいため、資産運用に使うには
リスクが大きすぎるといえます。
このグラフの場合だと、バリュー平均法(青)がドルコスト平均法(緑)の
パフォーマンスを上回っていきます。
面白いのはバリュー平均で資産を売る際、
売却時にかかる税を引いたとしても
ドルコスト平均法を若干上回っていることです。
だとすると、課税口座をつかったとしても
バリュー平均を使ったほうがいいということ?
なかなかスゴイ威力です!
「いやいや、そんなきれいな右肩上がりだから上手く行ってるんじゃないか?」
という声も聞こえてきそうです。
でも、「右肩上がり1」のシミュレーションでは
ドルコスト平均法の方が良かったわけです。
もしかしたら大きく下がって一気に上がるような局面では
一時的にドルコスト平均法が上回るのかもしれません。
では、上がり下がりが全くない
横ばいの場合を見てみます。
3. 横ばい
バリュー経路を8千万までとすると
途中で銀行残高がマイナスになってしまうので、
6千万までとしました。
ドルコストの購入額は前回と変わりありません。
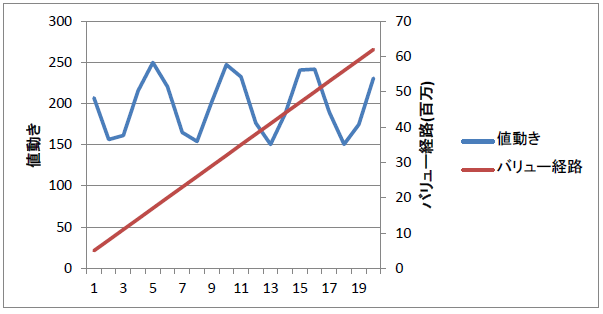
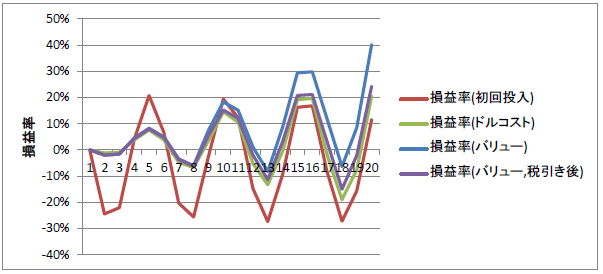
なんと横ばいであっても、
バリュー平均法のパフォーマンスは卓越していて
初回投入比+30%となっています。
課税口座を想定した税金を引いても、
ドルコストを上回っています。
うーん、すごいな。バリュー平均法。
バリュー平均法の死角
シミュレーションしていて思ったのは
確かにバリュー平均法は威力がありそうだ、
ということ。
前述のとおり、課税口座を使っても
バイ&ホールドのドルコスト平均法を
上回るパフォーマンスだったのはかなりの驚きでした。
いままでドルコストがいいと思っていましたが、
ここまでいい結果が得られるなら
本気で検討しないといけません。
一方で、バリュー平均法には難しい面もあります。
一番厄介なのは
「バリュー経路をどうとるか?」
という点。
上のシミュレーションでも、バリュー経路を上げ過ぎると
途中で投資資金が枯渇する場合があることを確認しました。
投資資金がどうなっていくかは
投資対象資産の値動きに依存するため、
あらかじめ最適なバリュー経路を決めることができないわけです。
これについての現実的な解は
- 投資資金に応じたバリュー経路
を決めて、
- 投資資金が枯渇したら積みましはなし
あるいは
- 投資資金の上限を決めておく
というぐらいしか、方法は無いかなぁ?
投資資金に上限を決める点については
岡本氏の著書でも指摘されていましたので
恐らく運用の現場でもそうした対応がなされていると
推測されます。
それからもちろん、
今回のシミュレーションでは対象資産の値動きは
架空のものであり、かつたったの3パターンしかありません。
これをもってバリュー平均法の良し悪しを
結論づけるのはいささか強引といわれても
仕方ないことと思います。
例えば今回の「右肩上がり1」のように
ドルコスト平均法が有利となるような
シミュレーションをそれこそ無数に
作ることは可能でしょう。
ただ、今までフワフワとした感覚としてしか
バリュー平均法を捉えられていなかったんですが
きわめて特定の一面とはいえ数値を元に把握し、
その価値の片鱗を理解できたのは収穫でした。
バリュー平均法、奥が深そうです。
もっと深く研究する価値がありそうな、
そんな「匂い」がします。
次は原著に当たってみるかな…


