「72の法則」と「115の法則」だけ知っていれば、複利の計算は暗算でほぼカバーできます。

年利回り(%)と、その利回りで複利運用したときに資産が2倍になるまでの年数を掛けると大体72になる
という法則、一度は聞いたことがあるのではないでしょうか。
今日はちょっと軽めに、72の法則と、幅を拡げる応用について考察してみました。
72の法則とその導出
72の法則はあくまでも近似ですので、厳密解とは違いがあります。
ただ、僕が思っていたよりもかなり近似解に近く、また、年利1%〜15%という実用域で使いやすい法則になっていることが分かりました。
まずは結論からですが、厳密解と72の法則(とおまけで69.3)を重ねたグラフです(両対数グラフ)。
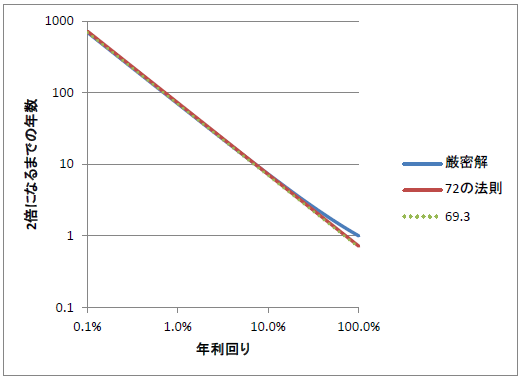
厳密解が青、72の法則が赤の実線ですが、年利15%程度までは、ほぼ重なっていて72の法則が優れた近似であることがうかがえます。
複利計算なのに、なぜここまでうまいこと重なるの?
と逆に疑問を持ってしまうぐらいですが、実際に計算してみるとこの謎が分かります。
年利xでy年、複利運用して2倍になるという式は
$$ (x+1)^y = 2$$
で表されますが、対数を取って式変形すると
$$ y \ln (x+1) = \ln 2 = 0.693$$
となります。
この時点でかなり72の法則に近づいていますが、
まだ
$$ \ln (x+1) $$
がじゃまですね。
そこで、テイラー展開で近似し、
$$ \ln$$
を取ってしまいましょう。
ここでポイントは「ゼロ付近」で近似するということです。
利回りは数%から十数%程度ですので、ざっくりゼロ付近でいいのです。
$$ \ln (x+1) = x + x^2 ...$$
と、非常に簡単な式になりますね。
エイッ!と思い切って直線(1次)で近似してしまえば
$$ y x = 0.693$$
という、72(0.72)の法則に近い式ができあがりました。
実際のx(利回り)にはパーセント値が入りますから、右辺は0.693ではなくて、69.3になります。
ではなぜ、69の法則にしなかったというと、それは諸説あって謎なようです。
ネットを検索すると、
- 実用で用いる10%付近の誤差を小さくしたかった(72は8%付近で最適化されている)
- 覚えやすい数字にしたかった
- 割り算しやすい数字で実用的
などの理由があげられています。
8%の最適化というのも8%±7%という、非常に実用的な領域を近似していて合理的かつ絶妙だなと思います。
それらの理由に加えて、僕が思うに「72がなんとなく、美しかった」というのもあったのではないでしょうか。
「美しい」という基準は、主観的で非論理的ですが、人々の間で物事が広がっていく理由として、「なんとなく美しい」とか、「なんとなく覚えやすい」という、ヒトの美的センスというのは絶対に無視できない要因だと個人的には思っています。
Wikipediaの72の法則によれば、15世紀のイタリアで既に知られていた法則のようですが、最初に発見(?)した人は素晴らしい美的センスの持ち主だったのではないでしょうか。
近似の方法も大胆かつ繊細で、かなりの教養の持ち主だったと推測されます。
イマドキ複利計算なんて金融電卓やExcelでチョチョイのチョイですから、72の法則自体、ほとんど無意味だという意見もあるようです。
が、僕が注目したいのは、電卓もExcelも当然なかった時代に、ここまで使いやすく、優れた近似を導出した人間の能力とセンスには感服せずにはいられない、ということ。
72という、たった一つの数字にも、人間の奥深い可能性を見いだせるのです。
シンプルで美しい法則なだけに、余計インパクトがありますね。
72と115の法則
さて、72という数字一つとっても知的興味は尽きないわけですが、ある程度実用的であってもらわないとね…という意見もあって、それはそのとおり。
72の法則は、それ単体でも十分役に立つのですが2(とその倍数)しか使えないという、もどかしさがあるのも事実です。
そこで、二番煎じで恐縮なのですが、「115」という数字も記しておきたいと思います。これは「資産が3倍になるまでの年数」を同様に計算するための数字です。
72同様、8%に最適化した114でもいいのですが、9%に最適化した115の方が覚えやすいかなと思い、ここでは115を挙げておきます。
例えば、年利5%で23年複利運用(5x23=115)すると、資産が3倍になるという近似が得られます。
これも近似ですので厳密解とは異なりますが、72と同様、年利1%〜15%程度までであれば無理なく使えます。
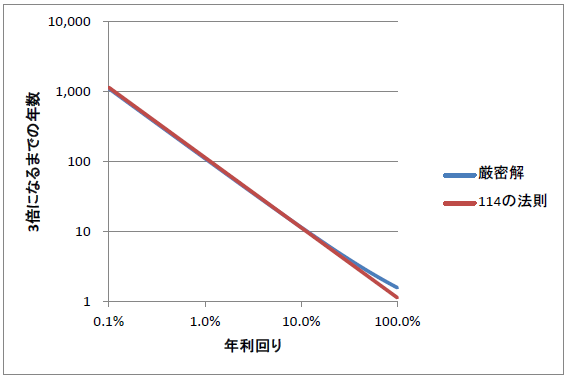
このグラフを見れば、72の法則とほぼ変わらない近似レベルなことが理解できるでしょう。
3倍になる年数が分かれば、2倍の年数と組み合わせることで
2倍=2倍(72の法則)
3倍=3倍(115の法則!)
4倍=2倍x2倍
6倍=2倍x3倍
8倍=2倍x2倍x2倍
9倍=3倍x3倍
…
と、計算の幅が格段に広がります。2と3というのは、とても便利な数字ですね。
例えば年利5%、複利で6倍になる年数を計算したければ、6=2x3なので、2倍になる年数と3倍になる年数を足せば資産が6倍になる年数が出ます。
2倍:72÷5=14.4
3倍:115÷5=23
両者を足して:14.4+23=37.4年という計算が簡単にできますね。
いずれも近似ですので、実用上はざっくり37年でいいでしょう。ちなみに5%、6倍の厳密解は36.7年でした。
これなら暗算か、スマホの電卓程度でできますので、会話の幅もグンと広がりそうですね!(ホントか?)
以上、取らぬ狸のなんとやらではありませんが、資産運用の豆知識でした。
長期運用は皮算用以上にコストが大事
利回りの計算はそれ自体で楽しいですが、特に長期の運用にあたってはコストの見積もりも大切です。
こちらの記事
個人型確定拠出年金(個人型DC/iDeCo)、運用商品とコストを徹底的に比較した結果…狙い目はココ!
なども、あわせて参考にしてください。
それと、当たり前なんだけど、でも実はあまり意識されていないのは、ちゃんと収支を見積って、余計なリスクを負わないようにする、というのが大事です。
具体的にはしっかりしたライフプランを作っておいて、運用益がなくても大丈夫であることを確認した上で、必要に応じて取れるリスクを取っていく、というアプローチが大切ですね。
これをしておかないと、ライフプラン上で苦しい時期に、運用の方も苦しくなった場合に破綻してしまう可能性が高くなってしまいます。
これでは、本末転倒ですよね。
とにかく長期投資は「やめずに続ける」ということが最も大事なポイントになってきますので、ライフプラン上で問題ないかどうかを先に見ておくのは必須条件と言えます。
ライフプランに関しては、こちらも参考にしてください。



「72の法則」と「115の法則」だけ知っていれば、複利の計算は暗算でほぼカバーできます。 https://t.co/XYcx4rIoly
RT @Ken_Invester: 「72の法則」と「115の法則」だけ知っていれば、複利の計算は暗算でほぼカバーできます。 https://t.co/XYcx4rIoly
こんにちは。72の法則について調べていてここまで詳しく、わかりやすく書いてあるところは他に見当たりません。テイラー展開が出てきた次点でムムッとなりましたw
少し気になったのですが、私の表示環境では文字化けしているのでご報告します。
年利$latex x$で$latex y$年、複利運用して2倍になるという式は
$latex (x+1)^y = 2$
M1さま
コメントおよびご指摘頂き、
ありがとうございました。
確かに、文字化けしていますね(汗)
なにかの拍子に、ワードプレスのプラグインが
機能しなくなっていたようです。
改善しましたので、よろしければ
もう一度読みやすい記事でお楽しみください!
林